🎯 시계열 데이터란?
시계열 데이터는 시간의 흐름에 따라 순차적으로 기록된 데이터를 의미합니다. 주식 가격, 일별 매출, 시간대별 웹사이트 트래픽 등이 대표적인 예입니다. 이러한 데이터는 시간에 따른 특별한 패턴과 특성을 가지고 있어 분석과 예측을 위해 특별한 접근 방식이 필요합니다.
“시간의 흐름에 따라 기록된 데이터”라는 간단한 정의 뒤에는 다양한 도전 과제와 흥미로운 패턴들이 숨어 있습니다. 이번 글에서는 시계열 데이터의 구성 요소 분석과 전처리 방법을 중심으로, 실전적인 관점에서 시계열 데이터를 다루는 방법을 살펴보겠습니다.
Part 1: 시계열 데이터 이해와 전처리
시계열 데이터의 구성요소 분해하기
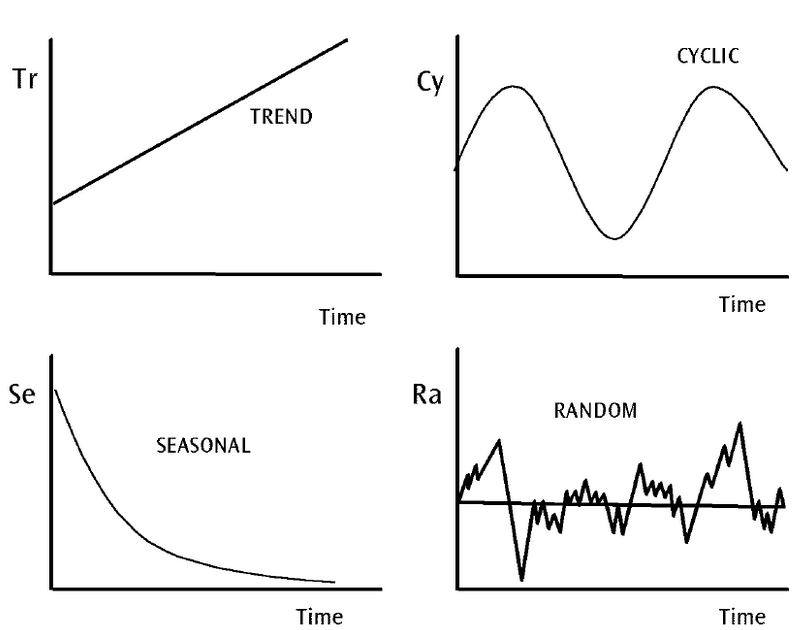
시계열 데이터는 마치 퍼즐처럼 여러 조각들로 이루어져 있습니다. 트렌드, 계절성, 순환, 노이즈의 네 가지 요소를 이해하는 것이 첫걸음입니다.
각각의 구성요소를 자세히 살펴보겠습니다.
- 트렌드(Trend): 데이터의 장기적인 변화 방향을 나타냅니다. 예를 들어 제품의 성장세나 시장의 전반적인 변화를 반영하는 경우가 많습니다.
- 계절성(Seasonality): 일정한 주기나 계절을 따르는 반복적인 패턴을 의미합니다. 예를 들어 여름철에 아이스크림 판매가 증가하거나, 특정 요일에 매출이 높아지는 패턴 등이 있습니다.
- 순환(Cycle): 경제나 시장 등의 큰 변화에 의해 발생하는 장기적인 변동 패턴을 의미합니다. 계절성과 달리 순환은 일정한 주기가 없고, 장기적인 경제적, 사회적 요인에 따라 달라집니다.
- 불규칙성(Irregularity/Random): 예측할 수 없는 외부 요인에 의해 발생하는 무작위적인 변동을 말합니다. 이는 데이터에서 불규칙적이고 임의적인 요소로 예측 모델에 영향을 줄 수 있습니다.
📌 매출 데이터에서 계절성과 트렌드를 분리하여 마케팅 캠페인 효과를 분석한 경험을 떠올려 보세요.
구성 요소 분해 방법
Python의 statsmodels 라이브러리에서 제공하는 seasonal_decompose를 사용하면 구성 요소를 쉽게 시각화 할 수 있습니다.
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt
result = seasonal_decompose(data, model='additive', period=12)
result.plot()
plt.show()
Tip: 시각화를 통해 데이터의 트렌드와 계절성을 확인하면, 불필요한 노이즈를 제거하거나 데이터 특성을 더 잘 이해할 수 있습니다.
정상성 검정과 변환
시계열 분석에서 가장 중요한 개념 중 하나는 ‘정상성(Stationarity)’입니다.
정상성이란 데이터의 평균과 분산이 시간에 따라 일정하게 유지되는 성질로, 이를 확보해야 안정적인 예측이 가능합니다.
정상성 검정:
- ADF Test (Augmented Dickey-Fuller Test): 정상성을 검정하는 대표적인 방법
- 비정상 시계열 데이터는 차분(Differencing)이나 로그 변환으로 변환합니다.
변환 방법:
- 차분 (Differencing): 연속된 관측치의 차이를 계산해 추세를 제거
- 1차 차분: 직전 값과의 차이 계산
- 계절 차분: 계절 주기만큼 이전 값과의 차이 계산
- 로그 변환: 분산을 안정화하고 지수적 트렌드를 선형화
- Box-Cox 변환: 데이터의 정규성과 분산의 안정성을 동시에 개선
from statsmodels.tsa.stattools import adfuller
import numpy as np
from scipy import stats
def check_stationarity(timeseries):
"""
시계열 데이터의 정상성을 검정하고 결과를 반환
"""
# Augmented Dickey-Fuller 테스트 수행
result = adfuller(timeseries.dropna())
print('Augmented Dickey-Fuller 테스트 결과:')
print(f'ADF 통계량: {result[0]:.4f}')
print(f'p-value: {result[1]:.4f}')
print('임계값:')
for key, value in result[4].items():
print(f'\t{key}: {value:.4f}')
# 정상성 여부 판단
is_stationary = result[1] < 0.05
return is_stationary
def make_stationary(timeseries):
"""
비정상 시계열을 정상화하는 다양한 변환 시도
"""
transforms = {}
# 1. 차분
transforms['difference'] = timeseries.diff().dropna()
# 2. 로그 변환
if (timeseries > 0).all():
transforms['log'] = np.log(timeseries)
# 3. Box-Cox 변환
if (timeseries > 0).all():
transformed_data, lambda_param = stats.boxcox(timeseries)
transforms['boxcox'] = pd.Series(transformed_data, index=timeseries.index)
# 각 변환된 시리즈의 정상성 검정
results = {}
for name, transformed in transforms.items():
is_stationary = check_stationarity(transformed)
results[name] = {
'data': transformed,
'is_stationary': is_stationary
}
return results
# 원본 데이터의 정상성 검정
print("원본 데이터 정상성 검정:")
original_stationary = check_stationarity(df['value'])
# 필요한 경우 변환 수행
if not original_stationary:
print("\n비정상 시계열 변환 시도:")
transformations = make_stationary(df['value'])
# 결과 출력
for name, result in transformations.items():
print(f"\n{name} 변환 결과:")
print(f"정상성 획득: {'성공' if result['is_stationary'] else '실패'}")
실패 사례: 정상성 검정 없이 예측 모델링에 바로 들어가면, 데이터의 내재적 특성을 제대로 반영하지 못해 예측력이 낮아질 수 있습니다.
정리하며
시계열 데이터 분석은 기초 작업이 가장 중요합니다. 데이터의 구성 요소를 분해하고, 적절한 전처리를 통해 정상성을 확보하면 보다 정교한 모델링이 가능합니다.
다음 파트에서는, 이렇게 전처리된 데이터를 활용해 ARIMA, SARIMA, Prophet 등 다양한 예측 모델을 적용하고, 비즈니스 활용 방안을 탐구할 예정입니다. 준비되셨나요? 😊